前面一篇文章讲解了DFS的基本概念和基础的使用方法，但不够深入，DFS的应用是很广泛的，不论是枚举状态或者路径，还是递归，其本质上都是DFS。今天就来好好的理解一下DFS的内在本质，并学会在树，在图以及在回溯中的应用。

回顾DFS

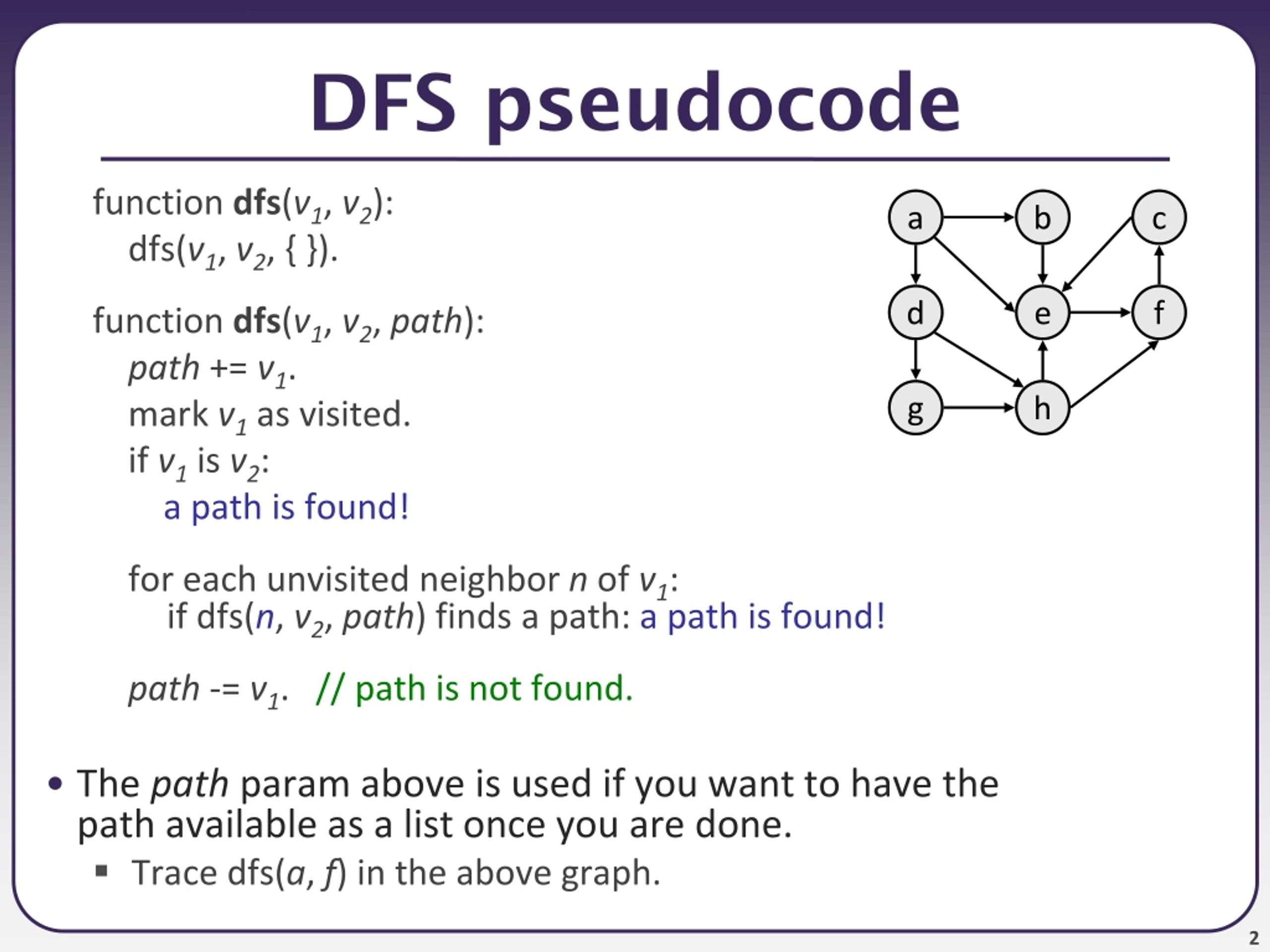
深度优先搜索，是指沿着某一路径方向，一直遍历到叶子节点为止，然后再回到初始顶点，换个方向继续。

这里就不过多的重复了，因为在前一篇文章里面已经讲过了，看那篇文章就好。

注意理解DFS的本质，DFS的本质就是递归，因此用递归式的DFS效率是最高的，如果是迭代式则要借助栈，伪码参见前一篇文章。

DFS树的遍历

树的常规遍历，涉及路径的问题，如查找 某一个路径，或者查找所有的路径都非常适合用DFS，效率也非常的高。

对于涉及树的层序的时候，如果是寻找层级内的某种状态，如层和，层最大值层最小值等，也是可以用DFS的。这方面可以参考前面的文章，以及关于二叉树的文章。

典型题目

路径问题

寻找特定的路径，或者枚举所有可能的路径就非常适合用DFS来求解。这其实是回溯算法，回溯其实就是用递归来枚举所有状态，这也是DFS的本质。

典型题目

图的遍历

典型题目

有返回值的DFS

有返回值的情况略为复杂，常规的DFS，特别是递归式，只以标记当成返回结果的，函数本身并没有返回值，但有时候光做标记还不够，还需要额外的信息作为是否有解的判断，这时就需要额外的返回值，通常用dfs函数的返回值作为判断。

写返回值时就要小心一些，当超过边界了，或者确定无解的情况下时返回无解状态（如false），DFS过程中已标记过了的地方直接返回有解（如true），然后递归 调用，并把递归 的所有结果合并起来当作 返回值。这里特别要注意的是要把下一步都递归了，再合并结果，因为DFS除了有返回值外，它还会做标记，如果简单的进行与，会因为布尔操作符的short-circuit原因导致某些分支没走下去，最后的标记状态肯定就不对。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

private fun dfs(g: Array<IntArray>, i: Int, j: Int): Boolean {
    if (i < 0 || i >= g.size || j < 0 || j >= g[0].size) {
        return false
    }

    if (g[i][j] == 1) {
        return true
    }
    g[i][j] = 1

    val n = dfs(g, i - 1, j)
    val w = dfs(g, i, j - 1)
    val s = dfs(g, i + 1, j)
    val e = dfs(g, i, j + 1)
    return n && w && s && e
}

典型题目

着色法DFS

典型题目

枚举+DFS（回溯）

如前所述，DFS的本质就是枚举所有状态，这其实也是回溯算法的核心所在，关于回溯可以参考另外的文章。

这类题目通常涉及矩阵或者可转化为图，用DFS进行暴力搜索（暴力穷举所有可能的路径），再辅以其他方法进行剪枝优化。

典型题目

参考资料

• DFS (Depth First Search) algorithm
• Learn Depth-First Search(DFS) Algorithm From Scratch