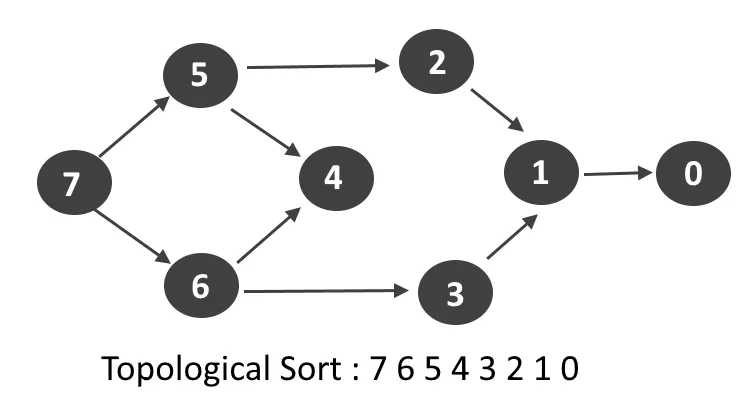
拓扑排序(Topological Sorting)是指将一个有向无环图(Directed Acyclic Graph)的所有顶点排成一个线性序列,使得图中的起始节点总是排在终止节点的前面,这是有向图每一个边都有起始节点和终止节点。这个名字有点容易混淆,它跟排序算法没有任何关系,拓扑排序仅是针对有向无环图,找到所有节点的一个可达的线性顺序。
关于图的基本概念可以参阅这个文章。
理解拓扑排序
拓扑排序是针对有向无环图才有意义,它是有向无环图所有顶点的一个线性序列,每个顶点只出现一次,所有顶点都要出现,如果有一条边是从顶点v[i]到v[j]的,那么在拓扑排序中v[i]一定要排在v[j]的前面。

有向无环图不一定存在拓扑排序,比如图不是全连通的,有些节点之间没有路径连接。但存在拓扑排序的一定是有向无环图,因此拓扑排序可以用来验证一个图是否是有向无环图。
拓扑排序的意义
拓扑排序通常代表着顶点之间的依赖关系,比如软件库的依赖关系,比如课程之间的依赖关系,比如任务调度中的依赖关系等,拓扑排序能够保证任务正确执行,被依赖的肯定 能先执行完,两个顶点(代表的任务)要么是有依赖关系的,要么是没有关系的,在拓扑排序中肯定 不会存在依赖错乱。
拓扑排序的实现方法
借助BFS可以实现拓扑排序。
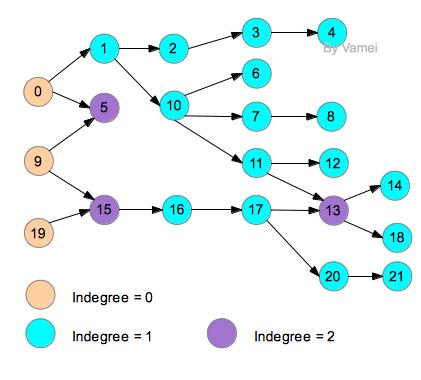
实现思路
- 先计算顶点的入度,入度是针对 有向图而言的,以顶点为终点的边的数量称为顶点的入度
- 从入度为为0的顶点开始,把它放入队列
- 每次从队列中取出顶点,打印出来。然后把这个节点所能直接连通的节点入度减1,并取出入度为0的顶点放入队列
- 重复第3步,直到没有入度为0的顶点,这时应该所有顶点都遍历到了,如果还有剩余顶点,说明有环
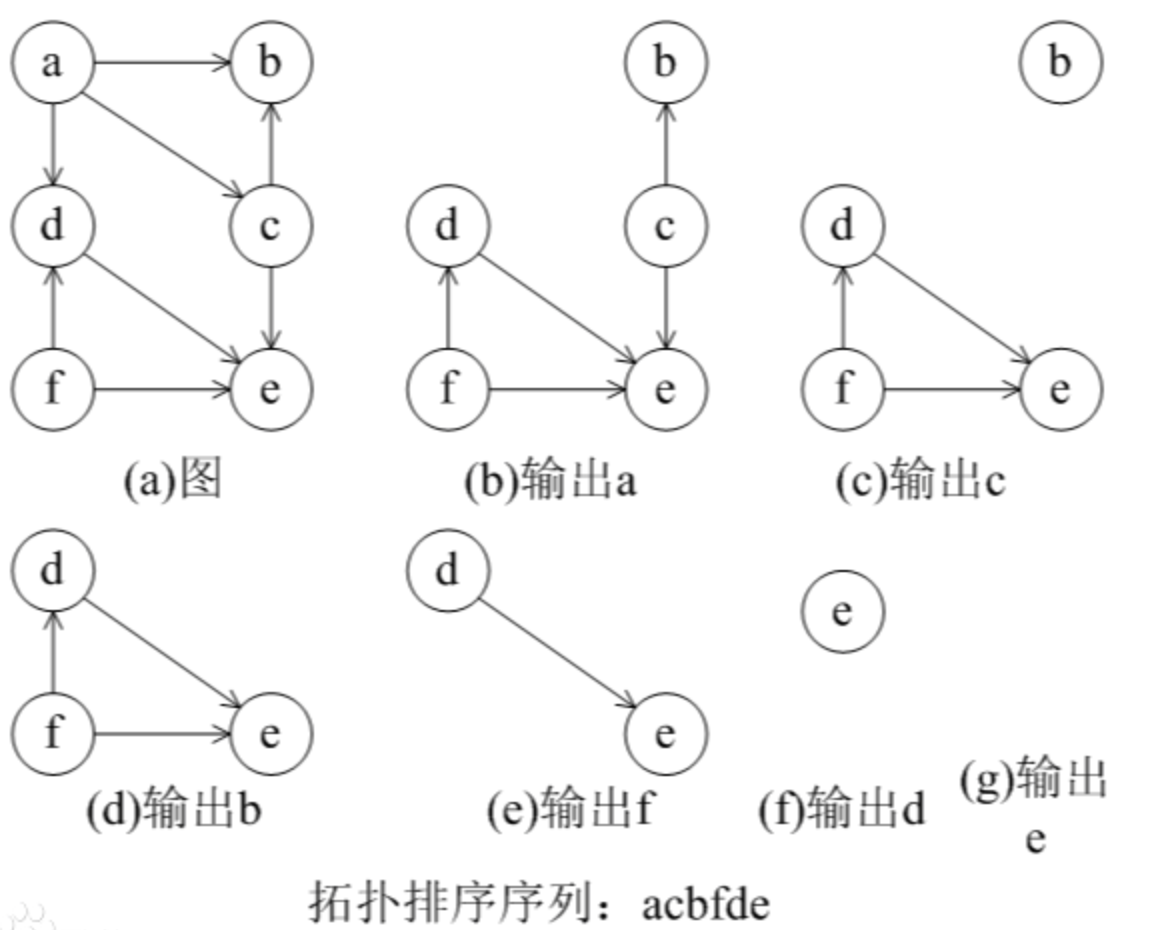
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | |
典型题目
| 题目 | 题解 | 说明 |
|---|---|---|
| 207. 课程表 | 题解 | |
| 210. 课程表 II | 题解 | |
| 329. 矩阵中的最长递增路径 | 题解 | |
| 剑指 Offer II 115. 重建序列 | 题解 | |
| 802. 找到最终的安全状态 | 题解 | 先求反图,再拓朴排序 |
| 1203. 项目管理 | 题解 | 挖掘隐藏条件,组间也有依赖,由项目的依赖推导出组间的依赖 |
| 1857. 有向图中最大颜色值 | 题解 | 拓朴排序过程也是在遍历图,可以顺便做遍历可以做的事情 |
| 题解 |