Binary Search Made Easy

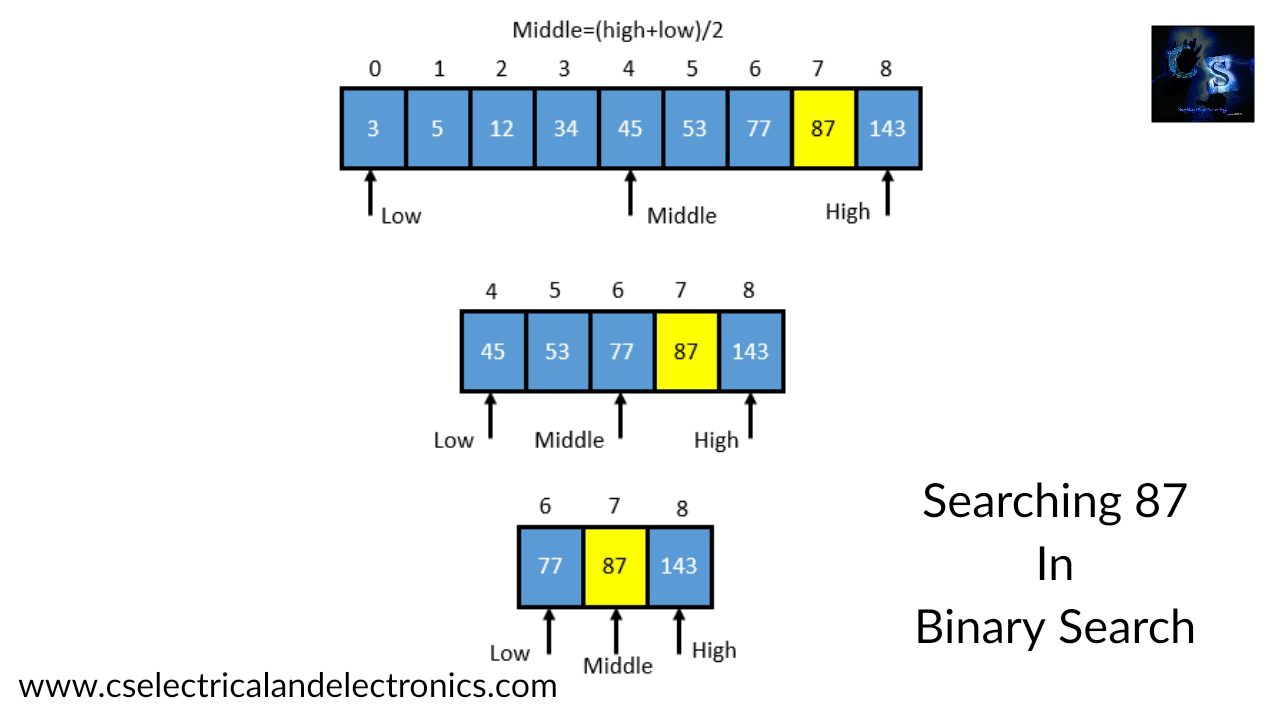
二分查找 Binary Search是效率特别高的一种算法，它能将线性复杂度O(n)降低到对数级别O(logⁿ)。但它对输入数据有要求，比如对于数组来说必须是排序的，否则是不能应用二分的。今天就来理解一下二分查找，然后总结常见的题目和注意事项。

理解二分查找

二分查找的特点是每次能把输入数据分成一半，这样不断的二分下去，直到只剩下一个。所以能应用二分查找的最重要的条件是要能够依据某种条件把输入数据分为两段，最常见的是排序数组查找，但并不限于这个，只要能依据某种条件把数据分成二份，就可以应用二分查找，比如数据是某种情况下的单调性？或者数据有明显的断崖，或者数据是山峰形状的，或者是山谷形状的都可以应用二分查找。二分查找博大精深，需要好好体会其二分的内涵。

对于升序排序数组查找的标准二分代码模板，二分查找模板题是704：

int left = 0;
int right = n - 1;
while (left <= right) {
    int mid = left + ((right - left) >> 1);
    if (nums[mid] == target) {
        return mid;
    } else if (nums[mid] > target) {
        right = mid - 1;
    } else {
        left = mid + 1;
    }
}
return -1;

标准二分典型题目

标准二分的意思是在一个有序数组中查找某个目标，也就是看目标在与不在，这个是可以应用标准二分模板的。

题目	题解	说明
74. 搜索二维矩阵	题解	矩阵中的二分
167. 两数之和 II - 输入有序数组	题解	标准二分查找
700. 二叉搜索树中的搜索	题解	BST中的二分查找
704. 二分查找	题解	二分查找模板题
1346. 检查整数及其两倍数是否存在	题解
367. 有效的完全平方数	题解
374. 猜数字大小	题解
	题解
	题解

防止溢出

注意事项就是，区间的开闭，以及中间索引的计算。循环的退出条件一般都是有等号的left <= right时循环。

对于有些情况索引会特别的大，造成计算中间索引时会发生溢出，这时就要先减后加，以防溢出：

int mid = left + ((right - left) >> 1);

// or

int mid = left + (right - left) / 2;

另外，这里的括号都不可省略，虽然移位符的优先级高于加法，但如果left等于right时，不加括号这个运算会出错。

题目	题解	说明
278. 第一个错误的版本	题解	如何防范溢出
	题解
	题解

非标准二分

有很多时候是用不上标准二分的，比如像寻找比某个数大的数（位置），寻找比某个数小的数（位置），数据仍然是有序的，依旧可以应用二分查找。

升序（非降序）中寻找第一个比目标大（不小于）的数

或者说寻找目标数在数组中的下界lower_bond，也即返回位置result前面的数都小于目标，result及其后面的数都不小于目标。

二分性的要点，第一个比目标大（不小于目标），那么假设arr[i]比目标大，那么arr[i-1]一定比目标小，所以当arr[mid]大于等于目标时向左找，否则向右找。返回第一个比目标大的索引。要注意无解的情况，就是当目标target比输入数组元素都大的情况时是无解的，这时返回-1。代码如下：

public int lowerBoundV1(int[] arr, int target) {
    int n = arr.length;
    int left = 0;
    int right = n - 1;
    // if need to return in loop, should use <=
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (arr[mid] >= target) {
            if (mid == 0 || arr[mid - 1] < target) {
                return mid;
            }
            right = mid - 1;
        } else {
            if (mid < n - 1 && arr[mid + 1] >= target) {
                return mid + 1;
            }
            left = mid + 1;
        }
    }

    return -1;
}

除了这样写，还可以用『完全二分』的方法来求解，可以参见后面『完全二分』部分。

题目	题解	说明
34. 在排序数组中查找元素的第一个和最后一个位置	题解
35. 搜索插入位置	题解
69. x 的平方根	题解
441. 排列硬币	题解
744. 寻找比目标字母大的最小字母	题解
878. 第 N 个神奇数字	题解
977. 有序数组的平方	题解
1201. 丑数 III	题解
1608. 特殊数组的特征值	题解
	题解
	题解
	题解

降序中寻找最后一个不小于目标的数

或者说寻找目标数在数组中的上界upper_bond。

本质上这与『升序中找第一个不小于目标的数是一样的』，可以用同样的套路来解：

public int upperBoundV1(int[] arr, int target) {
    int n = arr.length;
    int left = 0;
    int right = n - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (arr[mid] >= target) {
            if (mid == n - 1 || arr[mid + 1] < target) {
                return mid;
            }
            left = mid + 1;
        } else {
            if (mid > 0 && arr[mid - 1] >= target) {
                return mid - 1;
            }
            right = mid - 1;
        }
    }
    return -1;
}

题目	题解	说明
1855. 下标对中的最大距离	题解
	题解
	题解
	题解

区间二分

要寻找的目标并不是一个数值，而是一个区间，也是可以应用二分查找的。

题目	题解	说明
1385. 两个数组间的距离值	题解
	题解
	题解

断崖和山峰或者山谷

断崖也就是说数组分成两段，每段都是递增的；山峰也就是中间是最大向两边递减；山谷是中间最小向两边递增。这些数据都具有明显的二分性，都可以应用二分查找。整体思路不难，但要处理魔鬼细节。

典型题目

题目	题解	说明
33. 搜索旋转排序数组	题解	断崖式数组，注意二分条件
81. 搜索旋转排序数组 II	题解	去重后二分
153. 寻找旋转排序数组中的最小值	题解	断崖式数组，注意二分条件
154. 寻找旋转排序数组中的最小值 II	题解	去重复后二分
162. 寻找峰值	题解	山峰
658. 找到 K 个最接近的元素	题解	找第一个小于等x的位置
852. 山脉数组的峰顶索引	题解	山峰式数组
977. 有序数组的平方	题解	山谷形数组
	题解
	题解
	题解

二分库函数

二分查找是一个比较流行的算法，使用的也较多，因此绝大多数语言的标准库中都有此算法。

C语言：

#include <stdlib.h>

void *bsearch(const void *key, const void *base, size_t nitems, size_t size, int (*com)(const void *, const void *))

C++：

std::binary_search(start, end, target)
// *result >= target，*(result-1) < target
std::lower_bound(start, end, target)
// *result > target，*(result-1) <= target
std::upper_bound(start, end, target)

Java：

import java.util.Arrays;

int i = Arrays.binarySearch(arr, target);
// 返回是target所在的索引，或者其可以插入的索引的负值

Python3：

from bisect import bisect_left, bisect_right

left_most = bisect_left(arr, target)
right_most = bisect_right(arr, target)

Kotlin：

// binarySearch is an extension funtion of List
arr = listOf(1, 2, 3, 4, 5)
val i = arr.binarySearch(target)

完全二分

在大多数的二分查找中，我们说时间复杂度是O(logⁿ)，在算法分析中大O的意思是平均时间复杂度，但是很多二分查找是会提前退出的，因为会检查mid所在的元素是否满足，如果满足就终止查找过程了，所以很多时候真实运行的复杂度是小于logⁿ的。

但有些时候，是没有条件帮你判断可以提前退出的，必须不断的压缩区间范围直到只剩下最后一个元素，运行的时间复杂度一定达到logⁿ，这便是完全二分。

比如说寻找升序中比target大（不小于target）的第一个数，就可以用完全二分，来不断的压缩范围，直到最后一个就是答案：

public int lowerBoundV2(int[] arr, int target) {
    int left = 0;
    int right = arr.length - 1;
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (arr[mid] >= target) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return arr[left] >= target ? left : -1;
}

注意两点：1）不变式没有等号，当区间只剩下一个元素时停止不变式；2）注意无解的情况，即目标target大于所有元素时是无解的，这时要做检查然后返回-1；3）循环结束时left == right，这时用left或者用right是等价的。

数组是升序的，当索引mid大于等于target时，那么mid右边的数全都是大于等于target的，因为我们要找『第一个大于等于target』的索引，所以mid右边的都不可能是解，所以可以全部放弃，于是右界收缩到mid。如果mid小于target时，左边也肯定小于，所以左边，包括mid都不可能是解，因此左界收缩到mid+1。重复上述过程，直到只剩下一个元素，这时如果它满足条件（即大于等于target）那left/right就是答案，否则说明无解，返回-1。

可以加dump看一下，具体的执行过程：

target -> 3, len -> 9
arr = [ 1, 2, 3, 4, 5, 6, 7, 8, 9,]
  [mid] bigger than target, go left!
arr = [ 1, 2, 3, 4, 5,]
  [mid] bigger than target, go left!
arr = [ 1, 2, 3,]
  [mid] less than target, go right!
left/right -> 2, ans -> 2

target -> 10, len -> 9
arr = [ 1, 2, 3, 4, 5, 6, 7, 8, 9,]
  [mid] less than target, go right!
arr = [  ,  ,  ,  ,  , 6, 7, 8, 9,]
  [mid] less than target, go right!
arr = [  ,  ,  ,  ,  ,  ,  , 8, 9,]
  [mid] less than target, go right!
left/right -> 8, ans -> -1

同理，查找降序数组中最后一个大于等于target，也可以用完全二分来求解：

public int upperBoundV2(int[] arr, int target) {
        int left = 0;
        int right = arr.length - 1;
        while (left < right) {
            int mid = left + (right - left + 1) / 2;
            if (arr[mid] >= target) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }

        return arr[left] >= target ? left : -1;
    }
}

当mid大于等于target时，左边也肯定都大于，因为数组是降序的，所以左界收缩到mid；当mid小于target时，右边肯定也小于，所以右界收缩到mid-1。注意与升序找最后不一样的地方在于计算中间索引时要向右取整。

完整代码看这里。

还需要注意的是，要根据题目的要求进行调整以便让代码简洁方便，如果结果的判定较为繁琐，那就应该让最后一个元素时也能走进循环不变式，以让循环不变式中的条件进行判断。以及说无解时是返回左界-1，还是右界n，要看哪个更方便。题34就是很好的例子。

题目	题解	说明
436. 寻找右区间	题解
528. 按权重随机选择	题解
611. 有效三角形的个数	题解
981. 基于时间的键值存储	题解	找最后一个小于等于目标的元素，注意数组只有一个元素的情况
1146. 快照数组	题解	同981
1498. 满足条件的子序列数目	题解
2300. 咒语和药水的成功对数	题解
2476. 二叉搜索树最近节点查询	题解	树可能不平衡，所以转成数组用二分最稳妥
	题解
	题解
	题解

高难度二分

高难度二分的难点在于如何找到数据的二分性，也就是如何看待数据，以及如何找条条件以让其能具有二分性，这是应用二分的前提，具体情况比较繁多，视具体的数据类型与范围而定，没有明确的范式可以归纳，只能稍作总结。

题目	题解	说明
4. 寻找两个正序数组的中位数	题解
287. 寻找重复数	题解
300. 最长递增子序列	题解	状态定义很Tricky
354. 俄罗斯套娃信封问题	题解	状态定义很Tricky
410. 分割数组的最大值	题解
540. 有序数组中的单一元素	题解
1539. 第 k 个缺失的正整数	题解
1964. 找出到每个位置为止最长的有效障碍赛跑路线	题解	仔细体会与题300的差异，lowerBound与upperBound的差异
2071. 你可以安排的最多任务数目	题解
2576. 求出最多标记下标	题解
	题解
	题解
	题解

区间开闭和边界检查

二分查找思路并不难，但它有魔鬼细节，比如说区间是用开的，还是闭的，比如循环不变式到底要不要用等于，再比如要不要检查数组的边界，我们来稍作总结一下：

输入区间只能半开半闭，最好全是闭区间

二分查找必须界定一个查找区间，这个区间必须有一端是闭的，至于另外一端可开可闭，但最好全是闭区间。

如果是半开半闭，那么循环不变式终止条件一定不能有等于号。

循环不变式的终止条件

如果没有等于号，那么循环不变式终止时，左右界相等，指向同一个元素，循环不变式最后一次循环体内，左历界指向一对相邻的元素；

同理，如果有等于号，终止时左界超过右界，最后一次循环时左右界相等指向同一元素。

所以，这里就没有固定范式了，取决于你在循环体内进行什么样的判断，如果你多判断了前后的元素，那么开式（不带等号）也是对的。

一般的建议：区间闭，循环体内有return时一定用闭式（带等号的），因为循环体内有return，必须要检查是否有结果返回，而只有闭区间才能保证每个元素都检查到，开区间时当区间只有一个元素时是走不进循环的；而完全二分压缩区间时用开的，这是因为完全二分是要不断的压缩区间直至只剩下一个元素，当然你用闭的也可以，只不过最后把left-1当成答案。

稀有猿诉

十年磨一剑，历炼出锋芒，说话千百句，不如码二行。